Ken Ring can’t predict earthquakes either - by David Winter

 Borrowed from http://sciblogs.co.nz/the-atavism/2011/03/01/ken-ring-cant-predict-earthquakes-either/

The New Zealand media have done a remarkably good job of covering the
Christchurch earthquake. TV, newspapers and radio have all struck the
difficult balance between the country’s desperate need to understand
what happened on the 22nd and how people are coping with the right that
each victim the quake has to privacy in such a terrible time. The media
have also shown great restraint with respect to one particular story.
Ken Ring, the astrological weather forecaster, claims to have predicted
the earthquake. I think Ring, with all his calculations and post-hoc
explanations, is the very embodiment of what Richard Feynmann called “cargo cult science”
– someone who does some of the things scientists do, but fails in the
most defining characteristic by not honestly testing his theories
against data. I’ve had a little fun at his expense before,
but, really; as much as it makes me sad that we live in a world in
which Ken Ring can sell his weather forecasts and appear as an “expert”
on anything in the media, the worst thing his almanac does is take money
from people. In the wake the earthquake Ken Ring has done something much more serious. While thousands of people are devastated by a natural disaster, and terrified about what might happen next, Ken Ring claims to have predicted the earthquake of the 22nd and that a much worse one is due in March. So, let’s do what Ring fails to and test his methods against reality.

If Ring had really made an isolated and specific prediction that a destructive earthquake would strike Christchurch on February the 22nd then he might be worth listening to. His claim revolves around this post from his website a little more than a week before the event. Here’s the quotes he’d like you to pick out from that post:

The window of 15-25 February should be potent for all types of tidal action, not only kingtides but cyclone development and ground movement.
Over the next 10 days a 7+ earthquake somewhere is very likely

You might quibble that the Christchurch quake, at magnitude 6.3, was about 5 times less powerful than the M7 event he’d predicted – but I don’t think anyone in Christchurch wants to argue about how strong their quake was. On the face it, it really does look like an amazing coincidence: Ring predicted a quake and it happened. But there is more to it than that, I’ve been through his site and Ring has also predicted earthquakes for, at least, the 24th of September, the 1st and 7th of October the first week in November, the 20th to the 27th of January, the 1st to the 5th and 19th to the 25th of March and the 17th of April. In fact, in one post, giving him the +/- one day he needs in order to claim he predicted the February 22nd quake , he paints more than half of the time between the start of January and the end of March as earthquake risk:

You can add a fair few false negatives to those false positives. In October he claimed the aftershock sequence would die down, missing the major rumble on boxing day and several times he declared that it was unlikely Christchurch would be face another major quake (tragically wrong).
Thanks to the way our brains work, we generally struggle to evaluate theories of causation and claims of prediction fairly. We are too impressed by occasional “hits” and tend to forget the many “misses” which outweigh them. If we want to be rigorous, how should we react to hearing about Ring’s “hit” given the litany of “misses” I list above? As it happens there is a theorem for that. Bayes theorem is one of the most important little pieces of maths going around, because it tells us how to update our beliefs about a given question in light of new evidence, and that’s exactly what we should be trying to do if we want to lead a skeptical life. It is maths, but it’s not too scary. I’m the sort of person that loses contact with scientific papers as soon as ‘Σ’s and ‘∫’s start turning up, so you know if I’m writing this , you can follow it. Before we start, we need to define a couple of terms. Let’s call P(KR) the probability Ken Ring can predict earthquakes and P(Prediction) the probability that Ken Ring would have successfully predicted this earthquake. From that we want to calculate how probable the claim “Ken Ring can predict earthquakes” is given his successful prediction, well call that P(KR|Prediction). Once we have those defined it’s just a little 3rd form algebra:

P(KR|Prediction) =	P(Prediction|KR) * P(KR)
	P(Prediction)

So, how are we going to replace those terms with numbers? For now, let’s not be one of those close minded skeptical types, ignore how eccentric Ring’s methods and takes the evidence as it stands by saying P(KR) is 50%. P(Prediction|KR) is the probability that Ring would have predicted this quake if his methods work. You might be tempted to says this is 100%, but remember, he missed the Boxing Day aftershock and he’s repeatedly said Christchurch was unlikely to be hit again, so he’s not immune to false negatives either, I’ll be generous and give him 90%. The really interesting bit in Bayes Theorem is the bottom term P(Prediction). If we are being agnostic about Ken Ring’s abilities then we need to estimate this with regard to both the possibility his method has something going for it and the possibility that it doesn’t. We’ve already said that Ring has an 90% chance of predicting an earthquake if his methods work, what’s his chance of ’successfully’ predicting a quake even if his methods don’t work? This is the most important question you should ask yourself about his claims and it’s where all those false alarms come in. Given the ‘calendar’ above, Ring would have claimed to have predicted the quake if it fell on any of half of the days between January and March. His prediction for February was a little more specific than that, but when you read the post it’s still quite vague: “somewhere”, “in the ring of fire”, “withing 500km of the Alpine fault”. I’m going to say, given the huge number of predictions he’s made, there was about a 30% chance any day that had an earthquake would have been one Ring had previously predicted. To get P(Prediction) we have to balance each scenario like this:

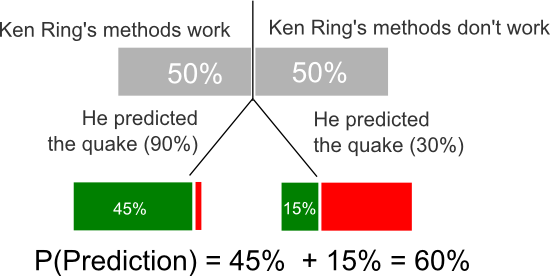
Now, when we put the numbers in like so…

P(KR|Prediction) =	0.9 * 0.5
	0.6

…we end up with P(KR|Prediction) being 75%. Ring’s successful prediction still supports the case that his methods work, but it’s hardly the decisive piece of information that allows us to say once and for all that he knows what he’s doing. You almost certainly want to put different numbers than I did in that equation, and you should. The idea is not to convince you a particular value is the right one, but to show you how including those false positives in our assessment of his claim changes the way we update our ideas about it and, by extension, how much stock we should put in his future predictions. There is a Bayesian calculator here for anyone that wants to play around with other numbers, over there P(H) is what we called P(KR), P(D|H) is P(Prediction|KR) and P(D|’H) is the probability Ken Ring got it right by mistake (the one I gave 30%).
Skeptics are often accused of being closed minded for sticking to scientific orthodoxy in the light some piece of evidence or other: “If you would just let this evidence stand by itself you’d see my theory is true!”. Assessing any evidence by itself, without our background of knowledge on a topic, is not being open minded – it’s being willfully ignorant. When we want to compare one theory to another we should use all the evidence available to us, and that includes what we know about how the world works. Ring thinks earthquakes happen when the moon makes its closest approach to the earth (called perigee) and around full and new moons. This next sentence really pains me, but here goes. His theory is not 100% lunacy. The phases of the moon have no effect on the earth, but the position of the moon in its orbit just might. As every schoolchild knows, the moon exerts a tidal force on the planet and there really are “land tides”, tiny swells and lulls in the crust of the earth analogous to the ocean’s tides, that ebb and flow through the day. It’s just possible that a fault that has been loading up with pressure for hundreds of years is more likely to give way when then moon is close and the tidal forces are stronger. But think about that for even a second and the problem becomes clear. Even if the moon is sometimes the straw that breaks the camels back at a particular fault, you couldn’t use the moon to predict an earthquake unless you already new a fault was about to go, i.e., the moon could only predict earthquakes when you could already predict an earthquake!
Ken Ring get’s a bit touchy about scientists dismissing his theories out of hand, so let’s look at some data. I actually asked Ring for some help with this, but he is yet to answer my email. Luckily, since the September 4th earthquake Paul Nicholls from Canterbury University has been plotting the intensity of the aftershock sequence. He’s also plotted the two lunar cycles Ring thinks are responsible for the strength of earthquakes: the lunar distance and the moon’s phase. In many ways, this is the data-set in which we are most likely to find support for Ring’s ideas. We know for a fact that the faults around the Canterbury plains are going to be under stress while the land sorts itself out after the upheaval in September. If the moon really was pushing already loaded faults past their breaking point we’d expect to see it in this data. Usually the most important statistical test you can perform on a data-set is having a look at it. This is Paul’s plot from last night, the slimmer of the two waves on the top represents moons orbit (troughs are perigee, the point Ring thinks is most dangerous) and the larger is the moon’s phase (the troughs are new moons).

If you can see any correlation between either of the lunar cycles you’re doing a lot better than me. I decided to dig a littler further, and plot the intensity of each day’s activity against each of the lunar cycles. First the phases of the moon. Remember, Ring thinks new and full moons are the most dangerous, so we expect a curved relationship higher at either end of the x-axis. We find no such thing (in fact, if anything, it’s more dangerous between the new and the full moon):

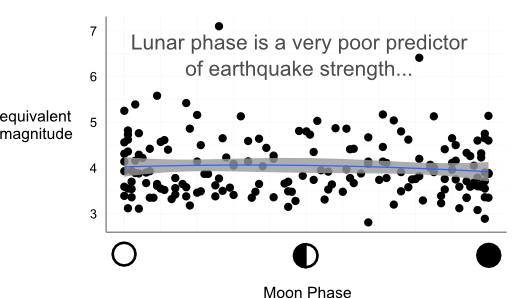
How about the distance between the earth and the moon? This is the one that makes just a little scientific sense:

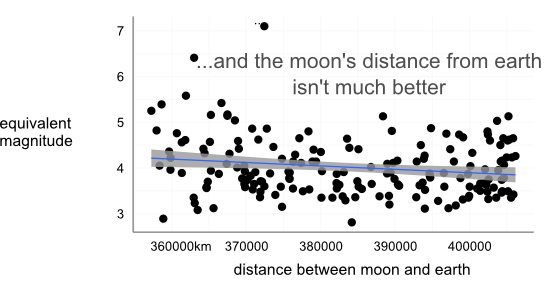
This time the relationship at least goes the right way, the quakes seem to be, on average, more powerful when the moon is close. In fact, when you put this data into a model that factors in the general tailing off in earthquake activity following the initial quake, the distance between the moon and the earth is a statistically significant variable with regard to the energy released. And there lies an incredibly important point. “Statistically significant” means unlikely to happen if the null hypothesis (in this case “the moon doesn’t effect earthquakes at all”) was true, it doesn’t mean the result is “powerful”, “meaningful”, or even “capable of explaining a great deal of the variation in the data”. As is often the case, we didn’t really believe our null hypothesis to start with, so it’s no surprise a large data-set found a significant relationship. But the actual effect of the moon is tiny, it explains about 2% of the variation in the data. The feebleness of the moon as a predictor is obvious when you look at the graph – there are plenty of days when the moon is close and there was not much energy released and, equally, there’s a whole lot of days when the moon was far away and there were still magnitude 5 quakes. The moon might well be having an effect on intensity of earthquakes from day to day, but if it can barely explain any of the variance in this data-set, one that was almost designed to test Ring’s theories in the best light, how could it predict an earthquake? It can’t.
Let’s get back to our calculation, last time we started with P(KR) at 50%. I hope you’ll agree, having seen the data, that Ken Ring’s methods are not the least bit plausible. I going to be outrageously generous and say there’s a one in one thousand chance that he can predict earthquakes, so let’s plug that into Bayes Theorem, remembering to update P(Prediction) for this new value too:

P(KR|Prediction) =	P(Prediction|KR) * P(KR)
	P(Prediction)
=	0.9 *0.001
	(0.9*0.001)+(0.3*0.999)

Which gives us a value of 3 in one thousand. Again, you’ll want to put different numbers into the equation, but there’s a really important point here. Whenever we hear evidence for some new claim, “a vaccine caused my child’s autism”, “light behaves as a particle and a wave”, “Ken Ring can predict earthquakes (and another one’s coming)”, we should use that evidence to update our prior knowledge of the world. Sometimes, like the outlandish claim that light can be a particle or a wave depending on how you look at, the evidence will be enough to completely change the we think, more often it will hardly make a blip. I think we can put Ken Ring firmly in the “hardly a blip” category: once you see how implausible his methods are you realise you’d need incredible evidence to believe his predictions and once you see his run of false positives you realise that his “prediction” of last week’s earthquake doesn’t meet that standard.
The people of Christchurch desperately need information. In the next few weeks they want to know if they’ll have to face the terror of last Tuesday again and once they city has pulled itself back up they’ll want to understand the future risks for the city. In a climate of such desperation people have a duty to provide only verifiable information and to explain that information’s limitations. That’s exactly what scientist from GNS and Canterbury University have done when they’ve spoken to the media. Ken Ring, who lambasted GNS for scaring people with a “knee jerk” comment that a magnitude 6 aftershock could be expected after the September earth quake, has not lived up to that duty and I really hope no one takes him seriously.